Sad news today: John Conway died from covid-19. Siobhan Roberts’s 2015 piece on him in the Guardian, John Horton Conway: the world’s most charismatic mathematician, is a wonderful introduction to his life and work:
Now 77, John Horton Conway is perhaps the world’s most lovable egomaniac. He is Archimedes, Mick Jagger, Salvador Dalí, and Richard Feynman, all rolled into one. He is one of the greatest living mathematicians, with a sly sense of humour, a polymath’s promiscuous curiosity, and a compulsion to explain everything about the world to everyone in it. According to Sir Michael Atiyah, former president of the Royal Society and arbiter of mathematical fashion, “Conway is the most magical mathematician in the world.”

I reviewed her biography Genius at Play: The Curious Mind of John Horton Conway when it came out in 2015:
Genius at Play: The Curious Mind of John Horton Conway, by Siobhan Roberts, is the best biography I’ve read in a while, and it’ll be in my top ten favourite books of 2015. Conway is a mathematician, an unruly digressive eccentric fascinating genius mathematician, and this is an unruly digressive eccentric fascinating biography, because no normal narrative structure (like Roberts used for her fine biography of straitlaced geometer Donald Coxeter) could get across what Conway is like. Conway’s such an unstoppable force he gets his own typeface in the book, so he can explain mathematics or tell a story or just interject.
This and her earlier book King of Infinite Space: Donald Coxeter, The Man Who Saved Geometry are two of the finest biographies of scientists and mathematicians that I’ve read. If you don’t know math don’t let that stop you: Roberts explains their work clearly for the lay reader, and even if you won’t come away ready to work on hyperdimensional geometry or surreal numbers you’ll get a decent sense of the math Conway and Coxeter did but also how their minds worked, which is utterly unlike most people.
This is especially true of Conway, who was an undeniable genius. I saw him give a talk in February 2002 at the Dedication of Geometric Polytope Mobile in honour of H.S.M. Coxeter’s 95th birthday. I don’t remember anything about the content of the talk, but I never forgot that I was staggered by how he talked about it: first some introduction, then he said something about the subject struck him as a bit curious and so he thought about it and made a new notation for it and then this and then that … and then we saw he’d gone into some unexpected area, found a new problem in math, and solved it, just from sheer curiosity and ingenuity.
At least, that’s how I remember it. I found my notes and this is what I wrote at the time (see also Wikipedia entries on Geoffrey Taylor, Alicia Boole Stott, polytopes and the great stellated dodecahedron):
Left work early on Friday and went to the Fields Institute to see the dedication of the statue for Coxeter’s 95th birthday. There were more than 200 people there, most young. Coxeter was in a wheelchair and looked ancient. He said he’d come from the hospital, where he’d been since passing out at a birthday party last week. He’s had prostate cancer and cancer of the eyelid (!) and that last was cured by radiation treatment that made his tear duct drain into his nose. He’s on his last legs, but his mind was still quite sharp. He told us a bit about Paul Donchian, who’d made the models of polyhedra and polytopes used in Regular Polytopes, and something about Sir Geoffrey Taylor, who’d introduced Coxeter to polytopes. He was the son of George Boole’s daughter, I think, and the nephew of a woman who married a Voynich who must be the one with the manuscript. Quite a family. Coxeter got a bit lost in some details, or forgot where he was in a story, but he certainly remembered his geometry.
Conway told a funny anecdote about Coxeter, and then went into polyhedra and how they can be greatened, stellated, or both, and Schäfli numbers and another kind of number. He moved up into polytopes and after an our he was well into some really interesting stuff that was what he’s thinking about these days. I can’t remember details. I could follow almost all of it, because he wasn’t going into a lot of detail, but I’d have to study it a bit more to get anything out of it. A fascinating lecture from a real genius. I hope he comes back to Toronto and I can see him again.
How smugly confident I was! “I’d have to study it a bit more to get anything out of it.” But this is true: “A fascinating lecture from a real genius.” He did come back to Toronto in 2004 for The Coxeter Legacy: Reflections and Projections, but I didn’t go to that. He wasn’t able to be at the book launch for Roberts’s biography, which I was lucky enough to attend, so the 2002 talk was the only time I saw him in person.

I’d known about him since I was a teenager, though, thanks to Martin Gardner’s “Mathematical Games” column in Scientific American, which I read in the magazine and in the book collections. That was where I learned about the Game of Life, and like everyone else with computer access I wrote programs so I could watch how shapes evolved. Mine I wrote on my Commodore PET 2001, which had 8K of RAM (yes: 8,192 bytes of memory). I recorded my investigations on index cards, which I still have.




Now that I look at these again decades later I see I couldn’t possibly have figured all that out. I must have been copying it from some other sources, like the back issues of Lifeline I got from Robert T. Wainwright in 1985, who sent me a very kind letter and answered some questions I had about patterns I couldn’t follow on my computer!
See the acorn on the LifeWiki for full details about the above figure.
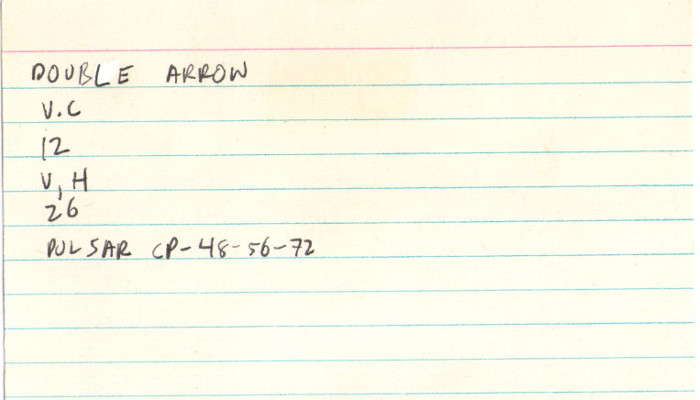

I don’t know where I got the name “double arrow.” This one I might have run on my computer, since it just lasted 26 generations before turning into a pulsar … but on further thought, probably not.

Life was just the first thing I learned about Conway. At university I read parts of On Numbers and Games and Winnings Ways for Your Mathematical Plays (which he wrote with Elwyn Berlekamp and Richard Guy) and got through most of Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness by the great wizard Donald Knuth on Conway’s work, which I still have on my shelf and will go at again. Even if the math got deep, Conway’s curiosity and delight and playfulness always came through.
About fifteen years ago I saw a video of a talk Conway gave about brick patterns.
I made some notes and have carried this around in my Filofax ever since:
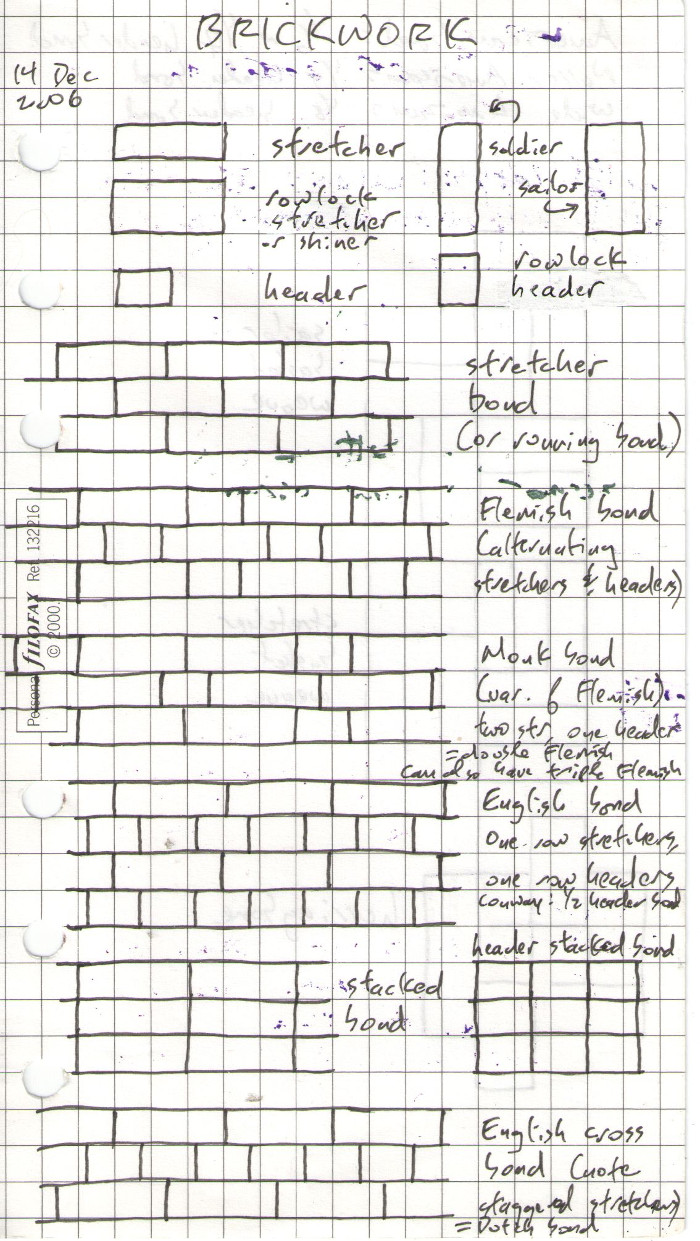
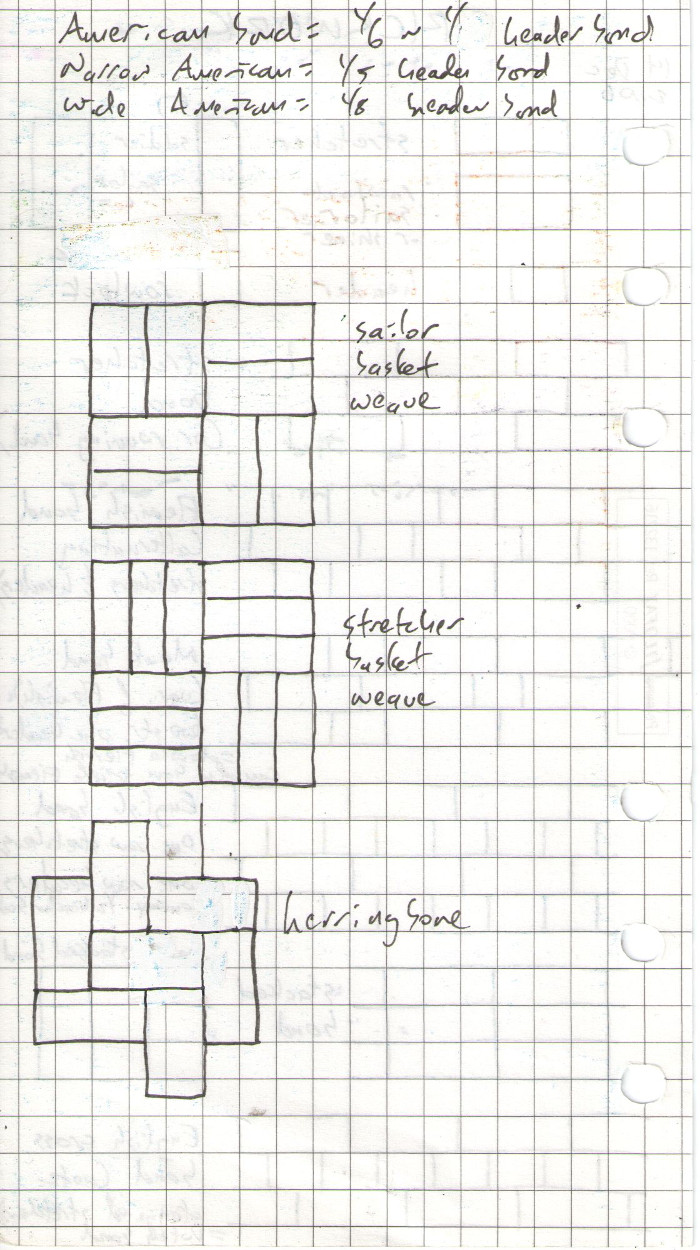
Most of the brickwork I see in Toronto is just veneer done in stretcher bond, but I always look to see if it’s not. If it isn’t, it’s usually American bond. See Wikipedia’s brickwork entry for more.
Finally there’s the Doomsday algorithm, which is a procedure Conway devised in 1973 to determine the day of the week for any date. A few years ago I learned it and would figure out what day things had happened on, which is idle fun, but knowing the doomsday is very helpful just to keep track of when things are in this calendar year: the doomsday for 2020 is Saturday, so right away I know Hallowe’en and Boxing Day are on Saturday. If someone says, “I wonder what day of the week May 24 is?” I think “May 9 is doomsday, so May 16 is also, so May 23 is also, so May 24 is the next day, Sunday.” Sure, you could look that up on your phone in a few seconds, but it’s good not to rely on your phone.
Here’s the algorithm I used, cribbed from Wikipedia:
Mnemonics for remembering the doomsdays in each month:
- January: 3 in common years, 4 in leap years (“the 3rd during 3 years in 4, and the 4th in the 4th”)
- February: last day (28 in common years, 29 in leap years)
- March: 7, 21 (first day of spring)
- April: 4 (even month)
- May: 9 (“I work from 9 to 5 at the 7-11”)
- June: 6 (even month)
- July: 11 (9 to 5 at the 7-11)
- August: 8 (even month)
- September: 5 (9 to 5 at the 7-11)
- October: 10 (even month; Hallowe’en)
- November: 7 (9 to 5 at the 7-11)
- December: 12 (even month; Boxing Day)
Find a year’s doomsday with the odd + 11 rule:
- Let T be the year’s last two digits.
- If T is odd, add 11.
- Let T = T/2.
- If T is odd, add 11.
- Let T = 7 - (T mod 7).
- Count forward T days from the century’s anchor day to get the year’s doomsday.
Anchor days by century (repeats every 400 years):
- 1800s: 5 (Friday)
- 1900s: 3 (Wednesday)
- 2000s: 2 (Tuesday)
- 2100s: 0 (Sunday)
Conway was born on 26 December 1937. What day of the year was that? Take 37; it’s odd, so add 11; that’s 48. Divide by 2; that’s 24. 24 mod 7 is 3. 7 - 3 is 4. The anchor day for the 1900s is Wednesday, day 3. Day 3 + day 4 = day 7 = day 0 mod 7, and day 0 is Sunday. So Conway was born on a Sunday, as cal shows:
$ cal dec 1937
December 1937
Su Mo Tu We Th Fr Sa
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28 29 30 31
John Conway, H.S.M. Coxeter, Martin Gardner and Rudy Rucker (see Gödel Rucker Ajzenstat from 2017) are the four mathematicians that had the biggest influence on me when I was a teenager.
I learned from them in the eighties and there’s something to learn from them now. Coxeter died in 2003 at 96, Gardner ten years ago at 85, Conway yesterday at 82; they all worked and thought and created right up to the very end. Rucker just turned 74 and continues to write and paint and document his life on his blog, and I hope will keep at it for many years more.
What I learned from them as a teenager is that mathematics is delightful and wondrous and infinite and mind-blowing and fun. What I learn from them in middle age—as I’ve learned from many others I admire—is to never stop working and thinking and creating.
 Miskatonic University Press
Miskatonic University Press